In this video we discuss how to calculate or determine how many classes to use, and how to calculate the class limits for a frequency distribution. Transcript/notes
How many classes and class limits for frequency distribution
In a past video we discussed what a frequency distribution is. Real quick, you have a data set, you break the data down into classes or intervals, column 1 which we will go in depth on in a minute, then you tally up how many data points are in each class, column 2, and you write that number down, which is the frequency, column 3.
So, how do we know how many classes to use and how to find the limits of each of the classes?
The first thing you have to determine is the number of classes. This number is usually between 5 and 20, the larger the data set, the more classes you should have, the number of classes is really about having enough of them to show patterns in the data.
There is no set in stone way to determine how many classes to use, but, one way is to use the equation 2 to the k is greater than or equal to n. Where k is what we want to find, the number of classes and n is the total number of data points in the data set, which in this case is 75.
Our main equation looks like this and we want to find the first time this equation becomes true, so we can start with 1, and plug in values for k. k=1, we get 2, k=2 we get 4, k=3 we get 8, k=4 we get 16, k=5 we get 32, k=6 we get 64, k=7 we get 128, ding ding. The equation is now true, so in this example we will use 7 classes.
Next we need to find the class width, and to do this we are going to use the equation width equals the range divided by the number of classes. The range is the difference between the highest value in the data set and the lowest value in the data set. In this data set the highest value is 466 and the lowest value is 126, so the range equals 466 – 126, which equals 340. Now we take that 340 and divide it by the number of classes, 7, and we get 48.57. We are going to round up to the nearest whole number, which is 49. So, 49 is our class width.
A little note, always round up when determining class width, for example if you calculated a class width to be 26.12, round up to 27. Rounding up is different than rounding off. And if you get a whole number with no decimal value as your class width, say you got 34, go up to the next whole number, 35, as this will give you enough space in the frequency distribution for all of the data values.
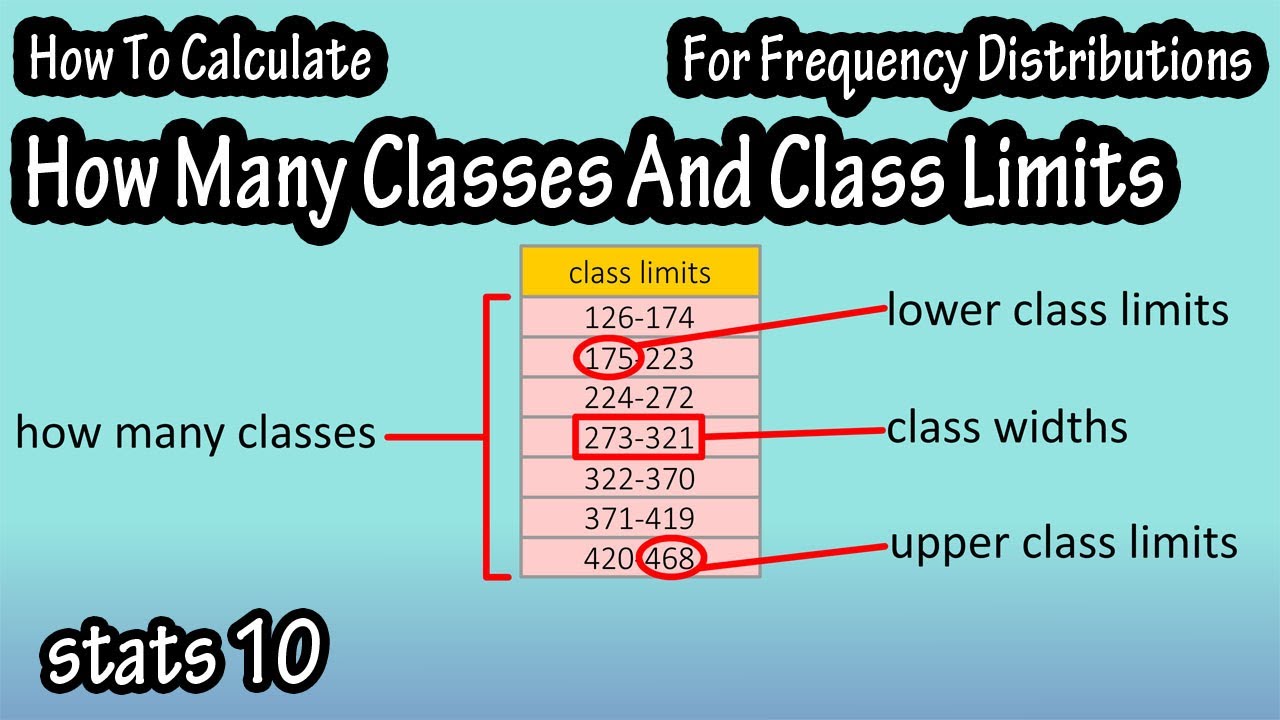
Next is to get a starting point for the lowest class limit. The minimum data entry is a convenient lower limit for the first class. In this data set that number is 126.
Next is to get the lower class limits for the remaining 6 classes, and to do this we just add the class width, 49 that we calculated earlier, to the value of the previous class’s lower limit. Again, the first classes lower limit is 126, the second classes lower limit would then be 126 + 49, which is 175. To get the lower limit for the third class, we take the lower limit of the second class, 175 and add the class width, 49, and get 224. And then continue this process to get the lower limits for the remaining 4 classes, 273, 322, 371, and 420.
To get the upper class limits for each of the classes, you subtract 1 from the next classes lower limit. So, for the upper limit of class 1, we will take the lower limit of class 2, 224 and subtract 1, which gives us 223. For the upper limit of class 2, we will take the lower limit of class 3, 273 and subtract 1, which gives us 272.
The next classes would be 322 – 1, 371 – 1, 420 – 1, and for the 7th and final class, since we don’t have a next class up to use the lower class limit from, we are going to take our lower class limit of the 7th class, 420 and add the class width of 49 and then subtract 1, which gives us 468.
So, now we have the class limits for all of our classes and we can organize them in a table like this.
Next you would tally up the data points in each of the classes, write that number in a frequency column, add in a relative frequency column, which basically shows you the percentages of values in each class, and walla, your frequency distribution is complete. I have another video that covers this process more in depth which I will link in the description below and at the end of this video.
0 Comments